Many people find mathematics hard or unintuitive. If there is any field of mathematics where that’s true, it’s probability theory. Unlike most other fields of mathematics, in probability theory, our intuition is actively harmful in learning it. You may think that “How many people have to be in the same room for there to be a 50-50 chance that two people in the room have the same birthday? The answer may surprise you!” is a clickbait title, but when it comes to probability, it is absolutely true (the answer is just 23).
Casinos and games of chance know how to exploit those wrong intuition. In many games of chance, it looks like you have a decent chance at winning, but once you do the math, you will never touch that game ever again.
I want to look at a very specific example of probability that we all probably have run into at some point in our RuneScape career: drop rates. A common misconception is that if something has a drop rate of 1/100 (say, Dragon Mattocks from Big Game Hunter encounters), you’re guaranteed to have one after 100 kills. This is not quite true. As a matter of fact, we expect only about two thirds of all people to get their mattock in the first 100 kills! This difference between expectation and outcome is the source of much frustration, since people believe that getting your first mattock after the first 100 kills should be near impossible. If that happens to you, you must be the unluckiest person in the world.
It isn’t difficult to understand why people think this. If the probability of getting your mattock in one drop is 1/100, then the probability of getting it after two drops is 2/100, right? This is where people go wrong, because you can’t just add your probabilities together. Let’s look at the simplest experiment: a coin flip. What is the chance that you roll heads at least once during two coin flips? That’s 75%, because there are four possible outcomes: first heads then tails, first tails then heads, or two heads or two tails in a row. In three of those four outcomes, there is at least one heads. Given that each of the outcomes is equally likely, the probability is 3 out of 4, or 75%.
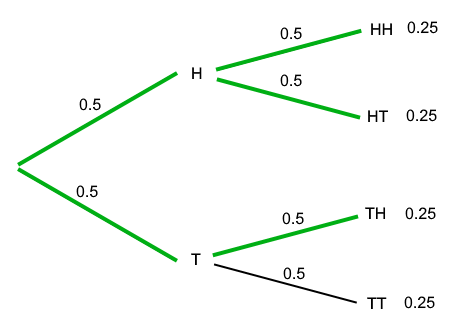
Coin flips are much simpler than mattock drops, because you don’t have a 50% chance of getting that drop. Let’s look at how we could have figured out the 75% for the coin flips without relying on the fact that every outcome is equally likely. For this, we can use a probability tree:
We start on the left. Here, we can go two different ways. These represent the two different outcomes of our experiment: up for heads, down for tails. After the first experiment, we can go up or down again, representing the outcome of our second coin toss. So each path we can take through this tree represents a possible outcome. So “first heads then tails” means going up the first branch, then going back down. At every point where the tree splits, we have a 50% chance of going up, and a 50% chance of going down. To get the probability of a given outcome, we just multiple the probabilities of all the branches on the way together. So for “first heads then tails”, we have 50% times 50%, which we often denote as 0.5 times 0.5, leading to a probability of 0.25, or 25%, which is correct! To get the answer of our original question of what the probability is of throwing heads at least once, we only have to add up all the probabilities of all the outcomes where we moved up at least once (marked with green in the image above), to get 0.25 + 0.25 + 0.25 = 0.75, exactly the answer we expected.
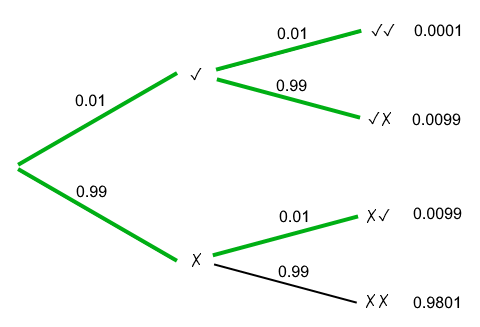
For mattock drops, we can use exactly the same strategy but the probabilities are different. Either we get a mattock (1%, or 0.01), or we don’t (the remaining 99%, or 0.99). To get the probability of getting at least one mattock out of two kills, we just need to add the probability of the three outcomes together: get two mattocks in a row, get a mattock on the first kill, and get a mattock on the second kill. Let’s put this in a probability tree again:
No we can easily figure out the probability, which is (0.01 * 0.01) + (0.99 * 0.01) + (0.01 * 0.99) = 0.0199, or 1.99%. That’s really close to 2/100, but not quite the same.
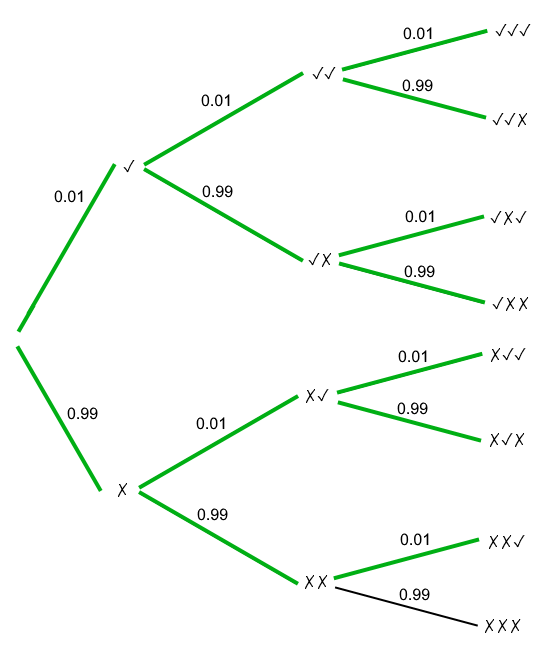
To really see why we don’t get even close to 100% chance on a mattock after 100 kills, we need to look at what happens after more kills. Let’s look at how the tree would look for three kills:
That’s getting a bit unwieldy. To get the probability of getting a mattock in three kills, we already need to add seven different outcomes together. If you look closely though, there is a trend going on. There is always only exactly one outcome that we want to not count: the outcome where we didn’t get a mattock on each drop. The probabilities of all outcomes must add up to 1. If we know the probability of not getting a mattock on every drop, we also know the probability of getting a mattock on at least one drop.
Getting the probability for not getting a mattock drop after some number of kills is easy: we always look at the probability of going on the down branch in the tree, namely 0.99. So for three kills, this is 0.99 * 0.99 * 0.99 ≈ 0.9703. To get the chance for at least 1 mattock drop, we look at 1 minus that number, so after three kills, you have slightly less than 3% chance of getting a mattock.
Let’s finally look at the probability of getting a mattock in the first 100 kills. For that, we first multiple 0.99 by itself 100 times, so 0.99100, which is roughly 0.366. So what is the probability of getting a mattock in your first 100 drops? 0.634, or 63.4%. Not quite the 100% many people hope for.
The “1 in 100” is always a bit misleading, but it is also true. If you do 1000 kills, you are expected to get around 10 mattocks. Just one of the ways that probability is counter-intuitive.
You can apply exactly the same method to other drop rates. What you will find though, is that you will always find that the probability that you get a 1/n drop in the first n kills for some number n is around 36.77%. The larger your n, the closer you will get. This phenomenon is called the law of truly large numbers (I am not making this up). So even if you couldn’t follow all the maths in this post, there is one simple result you can take away: if you don’t get your drop after the number of kills you expect, you’re just part of the unlucky third.